How did Graph Theory Start?
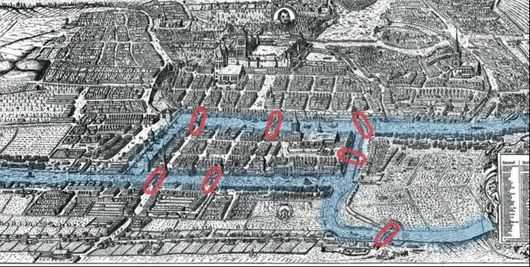
Leonhard Euler, a notable Swiss mathematician took a trip to the town of Königsberg in present day Russia. The city was significant to Euler because the presence of seven different bridges connecting the different four different landmasses. After some time Königsberg, Euler proposed an inquiry that asked if there was a way to walk to every part of town while crossing each bridge only once.
He constructed a series of points to represent each landmass with a connecting bridge. In addition, each connecting bridge became presented as a line from each of these points. When looking at the town in this manner, it can be shown that no matter which landmass you start on, there is no way to complete a path through the town in the way Euler desired. We can go through a process where we erase a line (or bridge) as we travel from point to point (or landmass to landmass) until we can no longer move to the next landmass without revisiting a bridge. This property that Euler observed later became known as an Euler Path. Thinking like this would become the basis for graph theory.
What is Graph Theory?
Graph theory is simply the study of graphs. A graph can be defined as G = (V,E) where V denotes the set vertices (or points) on a graph, and E represents the set of edges (or lines) on a graph.
In simpler terms, a graph is the presentation of a certain amount of vertices and edges. The vertex set is expressed as follows, V = {v0,v1,v2 ...,vn−1}, where each vi is a vertex for 0 ≤ i ≤ n and n is the number of vertices of G. Similarly, based off of the vertices, edges can be grouped into an edge set, (v0v1), (v1v2), (V2, ...). Now that we have an understanding of what vertices and edges are, we can begin to define other properties related to the graph, such as, the degree of a vertex. The degree of a vertex is simply how many edges connect to that vertex, i.e., how many edges are stemming off of it. Based upon these parts of a graph, mathematicians have studied what is now graph theory.
Vertex Coloring
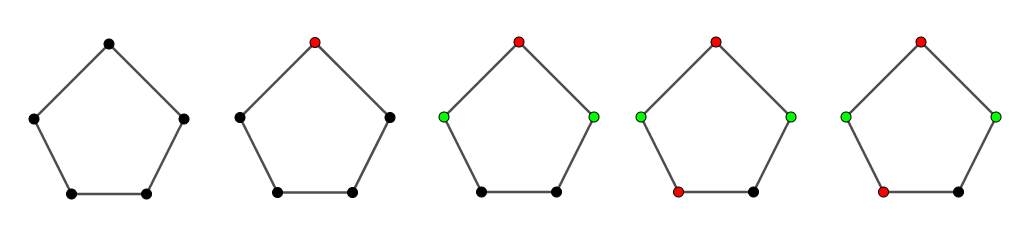
Another interesting property within graph theory is the notion of vertex coloring. Vertex coloring is the labeling of vertices in such a way that no adjacent (connected) vertices share the same color (see figure 5 and figure 6). The minimum amount of colors that can be used within this labeling is known as the chromatic number which can be written as χ(G).
We can begin the vertex coloring of a graph by picking an arbitrary vertex on the graph and coloring it red. Next, we label the two adjacent vertices extending from this arbitrary point with the color green. We can now arbitrarily choose to color one of the vertices adjacent to the last two colored vertices. One of the vertices extending from these points cannot be colored red because there is an odd amount of vertices on the graph. If both of these adjacent vertices are colored red, they will share the same color and disrupt the actual chromatic number of the graph. Because of this, we color one vertex red. We will choose to color the last vertex gray because it is adjacent to both a green and a red vertex. Since we had to use three separate colors within this graph because of the uneven number of vertices, our chromatic number has to be X(G) = 3.
We can begin the vertex coloring of a graph by picking an arbitrary vertex on the graph and coloring it red. Next, we label the two adjacent vertices extending from this arbitrary point with the color green. We can now arbitrarily choose to color one of the vertices adjacent to the last two colored vertices. One of the vertices extending from these points cannot be colored red because there is an odd amount of vertices on the graph. If both of these adjacent vertices are colored red, they will share the same color and disrupt the actual chromatic number of the graph. Because of this, we color one vertex red. We will choose to color the last vertex gray because it is adjacent to both a green and a red vertex. Since we had to use three separate colors within this graph because of the uneven number of vertices, our chromatic number has to be X(G) = 3.
What will I be doing?
In this research paper, we applied vertex colorings to simple family graphs and examined their basic properties. In addition to this, we also created our own graph along with its own infinite graph. The purpose of this research was to better understand graphs and their unique vertex coloring properties.